Since it took me a considerable amount of time to come up with how to answer this question to Stanford University’s Probabilistic Graphical Models 1: Representation course, I decided I would be posting it online. Not because I want people to copy and paste it to get a full grade, but because, for a couple of hours, I wanted the course to give me a more thorough explanation on how to approach the problem.
Consider the following model for traffic jams in a small town, which we assume can be caused by a car accident, or by a visit from the president (and the accompanying security motorcade).
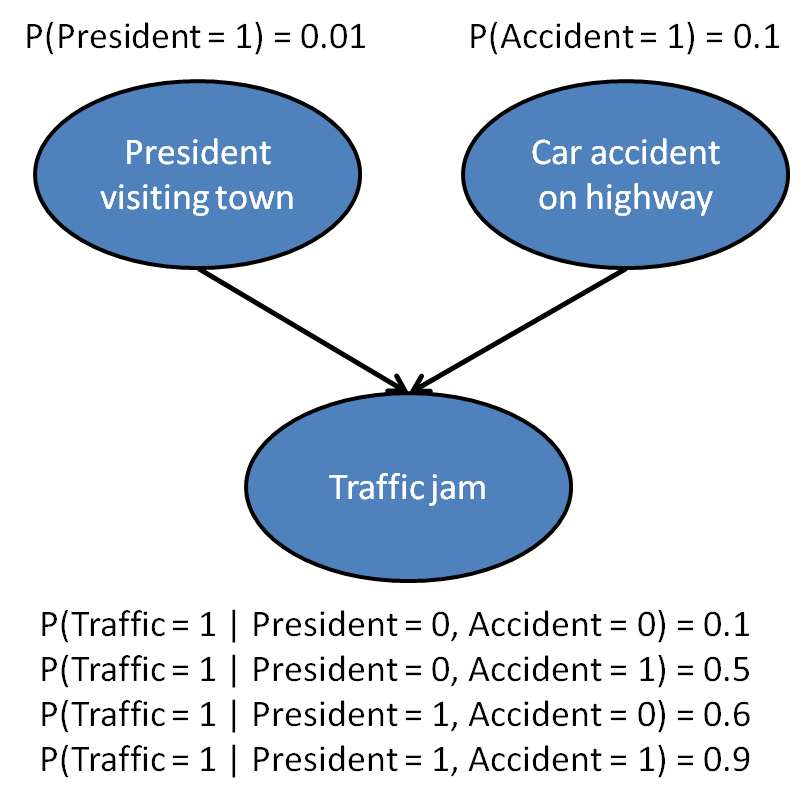 Created by Stanford University.
Created by Stanford University.
Calculate P(Accident = 1 | Traffic = 1) and P(Accident = 1 | Traffic = 1, President = 1). Separate your answers with a space, e.g., an answer of
0.15 0.25
means that P(Accident = 1 | Traffic = 1) = 0.15 and P(Accident = 1 | Traffic = 1, President = 1) = 0.25. Round your answers to two decimal places and write a leading zero, like in the example above.
What is given
P(P=1)=0.01P(P=0)=1−P(P=1)=0.99
P(A=1)=0.1P(A=0)=1−P(A=1)=0.9
P(T=1∣P=0,A=0)=0.1P(T=1∣P=0,A=1)=0.5P(T=1∣P=1,A=0)=0.6P(T=1∣P=1,A=1)=0.9
What is asked
- Given it was observed a traffic jam, what are the odds of having a car accident on highway
P(A=1∣T=1)=P(T=1)P(A=1,T=1)=0.14490.0504=0.3478261≈0.35
- Given it was observed a traffic jam and the president visit to town, what are the odds of having a car accident on highway
P(A=1∣T=1,P=1)=P(T=1,P=1)P(A=1,T=1,P=1)=0.00630.0009=0.1428571≈0.14
Development
P(A=1,T=1)=P(P=0,A=1,T=1)+P(P=1,A=1,T=1)=0.0495+0.0009=0.0504
P(P=0,A=1,T=1)=P(P=0)×P(A=1)×P(T=1∣P=0,A=1)=0.99×0.1×0.5=0.0495
P(P=1,A=1,T=1)=P(P=1)×P(A=1)×P(T=1∣P=1,A=1)=0.01×0.1×0.9=0.0009
P(T=1)=P(T=1,P=0,A=0)+P(T=1,P=0,A=1)+P(T=1,P=1,A=0)+P(T=1,P=1,A=1)=0.0891+0.0495+0.0054+0.0009=0.1449
P(T=1,P=0,A=0)=P(P=0)×P(A=0)×P(T=1∣P=0,A=0)=0.99×0.9×0.1=0.0891
P(T=1,P=0,A=1)=P(P=0)×P(A=1)×P(T=1∣P=0,A=1)=0.99×0.1×0.5=0.0495
P(T=1,P=1,A=0)=P(P=1)×P(A=0)×P(T=1∣P=1,A=0)=0.01×0.9×0.6=0.0054
P(T=1,P=1)=P(A=0,T=1,P=1)+P(A=1,T=1,P=1)=0.0054+0.0009=0.0063
Created by Stanford University.