Ruby numeric types: do’s and do not’s
In most programming languages, we have a whole range of numeric types. Ruby provide us 5 different of them:
- Fixnum
- Bignum
- Rational
- Float
- BigDecimal
Why?
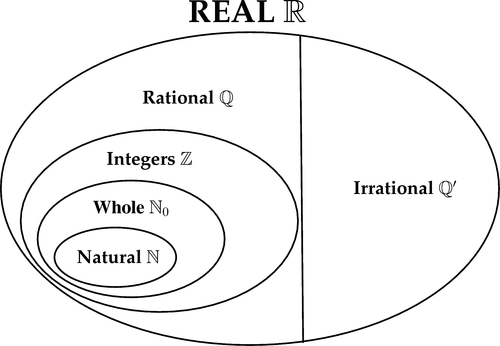
As everything in the world, we usually group numbers in different sets by their characteristics. The most common — and probably all you had contact while developing software — are the following: Natural numbers, Integers, Rationals and Irrationals.
Integers
Natural numbers are those, starting by 1 in a sequence that keep adding 1. Thus, 1, 2, 3, 4, 5, …. Integers are these same numbers but also includes this same summation to the opposite direction, 0, -1, -2, -3, -4, …. Ruby has a representation for this set: the abstract class Integer. Its concrete brothers are Fixnum and Bignum.
> 10.class
=> Fixnum
When you give an Integer literal (something that looks like an Integer) to the interpreter, the language will try to fit it into a Fixnum instance.
But sometimes this can’t happen. We have memory limit, since Ruby does not allow Fixnum’s bigger than a native machine word[1] (which varies between processors).
> integer = 2 ** (1.size * 8 - 2) - 1
=> 4611686018427387903
> integer.class
=> Fixnum
> integer = (integer + 1).class
=> Bignum
> (-integer - 2).class
=> Bignum
Isn’t the most daily task to deal with numbers greater than 4 quintillion, so you should be fine with Fixnum. If you change the value of a variable to a number out of the supported range (greater or lesser), Ruby will take care of freeing the memory used to hold the value and store it in another place. This last will be treated as an infinite allocation, so you may use it for basically any integer number you are able to come up.
[1]: Ruby core team is already taking care of defining an easier way to get maximum and minimum numbers fitting into a Fixnum object. Take a look: https://bugs.ruby-lang.org/issues/7517
Do’s and do not’s
It is hardly to expect numbers out of the range of Fixnum’s, or any smaller type for Integers provided by your language or database. If you’re using Ruby, just let it take care of the instantiation and use it in the most efficient way. Performing operations between Fixnum’s and Bignum’s will work fine and (after) will test for the possibility of using the simpler class for the result of calculations. In other words, the subtraction of two Bignum’s could result in a Fixnum, for instance.
Also, when using Integer literals in Ruby you can arbitrarily put underscores between the digits. It’s way easier to understand 129_990 than 129990.
Rationals
Unfortunately or not, we can’t represent everything just with Integers. Take the Integer 1 and divide it by 2. You can see the result in two different ways: simply 1/2 (as a valid operation but not capable of fitting into Integers set) or 0.5. Both of them are called “Rational”, since can be perfectly expressed by a ratio, or a division between Integers.
Ruby does provide a way to represent and perform calculations between Rational numbers, through the Rational class. In contrast to Fixnum/Bignum, Ruby will always assume you are expecting a Rational instance after calling mathematical functions using Integers and Rationals.
> Rational(1, 2)
=> (1/2)
> rational = Rational(1, 2) + Rational(1, 2)
=> (1/1)
> rational.class
=> Rational
> rational.to_i
=> 1
Rational numbers can also assume the same “Ruby form” as Irrationals.
Do’s and do not’s
Using the Rational class is especially useful when extremely important to have exact results but you don’t know about the form of numbers you are handling. If it’s likely to appear something that does not fit into Integers, enjoy the Rational class.
> 0.5r
=> (1/2)
If you’re going to have hard coded rationals, Ruby also helps you with literals. Write the number in the decimal form (that with the dot) and append a r.
Do not use it when having trouble with readableness and precision is not so important. If you are not sure if it is, assume it truth and later fix it. Your code can be modified, but precision may cause data to be lost forever.
Irrationals
Not all numbers can be expressed by ratios. But the same truth brings us good news: it doesn’t matter. When calculating the value of pi, we usually don’t need more than a couple of decimal places (even the real pi having infinite).
> Math::PI
=> 3.141592653589793
> Math::PI.class
Float
For representing Irrationals (and also Rationals) in Ruby, we have Floating Point numbers with its own arithmetic.
> (2.0 - 1.1) == 0.9
=> false
> (2.0 - 1.1)
=> 0.8999999999999999
> (2.0 - 1.1 + 1.1) == 2.0
=> true
This is a territory where even experienced software developers learned to not ask themselves so much. If you have some patience, you can understand better this set of numbers in IEEE 754.
WHY??!!! It’s so simple… in what world 2.0–1.1 would be different than 0.9 and how this thing got implemented in virtually every computer known?!
The reason is: should not matter! Floating point numbers, kindly called “Float” (homonym to its Ruby representation) imposes a limit for any number that could be really big or even infinite, but you don’t care so much about precision. For your use, doesn’t matter if the result is 0.8999999999999999 or 0.9. Both will get you happy and thanking this precious and big calculator you call “computer”.
> float = 0.00000000000000000000000000000000000000000000000000000000000009
=> 0.0
> float.class
Float
> float.zero?
=> true
Use any number with a dot as decimal place separator and Ruby will please you with a Float instance.
This happens because the standard defined by IEEE in 1985 (and in use by Ruby on its internals) stores the number in a limited precision. Even if you type 1 billion of decimal places, it won’t keep more than 15.
> 2.0 - 0.0000000000000006
=> 1.9999999999999993
In commands like 2.0–0.0000000000000006, you use a literal for the floating point number 2.0 and another for 1.1. The first will be stored as 2¹⁰ (2 squared to the 10th power) and the other… well, ask Wolfram|Alpha. Converting the number to base 2 (from base 10 we are used to) turns it into a really big problem. The calculation were made using two Float’s, so you expect a Float back, right? Ruby rounded the number as imagined to be acceptable for you. Since the 4 in the end doesn’t fit in its precision of 15 decimal places, it decided to turn the 4 into a 3.
If you need a little more precision but still doesn’t have to be exact as Rational, Ruby gives you the class BigDecimal. This last (internally) converts numbers to base 10000 (way harder to run “out of space”) and arbitrary precision.
> BigDecimal(‘500e1000’)
=> #<BigDecimal:7fc9c387e0d0,’0.5E1003’,9(18)>
> BigDecimal(‘500e1000’).to_f
=> Infinity
BigDecimal is the only number class without a literal form. It expects you to provide a string to initialize one. In my previous example, I gave the number I represented by 500 raised to the 1000th power. Trying to convert it to a Float, I get a whole new thing: Infinity. Ruby tried to fit it into its base/precision but noticed was out of range. “OK, this seems a valid number, but I can’t deal with it. It’s more than I can even imagine. It’s infinity!” Even not really being infinity, for the precision-careless Float, it is.
> 1 / 0.0
=> Infinity
> -1 / 0.0
=> -Infinity
The same occurs for out-of-range calculations. “I tried as far as I can, but it’s still something greater”.
> 0 / 0.0
=> NaN
> Float::INFINITY / Float::INFINITY
=> NaN
> 0 * Float::INFINITY
=> NaN
For calculations Float doesn’t even know how to start, it introduces the special value NaN, from “Not a Number”.
Do’s and do not’s
When 2.0 and 1.9999999999999999 means no harm to your user, take Float by hand and go happily walk on the yellow brick road. Otherwise, if you need to take control of roundings, consider other alternatives. Floating-point itself defines mechanisms of rounding, but doing it in a n-th decimal place won’t be a pleasant work. For use with currencies, which is always expected to have (only) 2 decimal places, the Integer 1000 can be interpreted by your business logic as $10.00.
Originally published at irio.tumblr.com.